고정 헤더 영역
상세 컨텐츠
본문

위험회피와 효용
사람마다 생긴 모습이 다르듯이 투자자마다 투자하려는 성향 또한 다르다. 기대이익과 위험에 대한 위험회피정도도 다르기 때문에 각기 다른 기대이익과 위험을 가진 포트폴리오에 대하여 점수를 부여, 선호도의 순위를 매긴 것을 효용(utility)이라고 한다. 즉, 효용이란 일종의 포트폴리오는 높은 점수를 얻고 높은 변동성(volatility)을 가진 포트폴리오는 낮은 점수를 얻는다. 일반적으로 기대이익과 위험, 그리고 투자자의 위험회피 정도를 고려한 효용의 공식은 다음과 같다.

이 효용의 공식은 재무관리나 투자론에서 효용, 기대이익률 위험 그리고 투자자의 위험회피정도를 나타낼 때 흔히 쓰이는 공식으로써 다음과 같은 특징을 갖는다.
첫째, 포트폴리오 분산이 클수록, 포트폴리오 분산이 작을수록 효용은 크다.
둘째, 같은 포트폴리오, 같은 포트폴리오 분산이라도 투자자의 위험회피 정도가 클수록 효용은 작아진다.
셋째, 위험회피 투자자일수록 투자자의 위험회피 정도가 크다.
넷째, 투자자는 효용이 가장 큰 포트폴리오를 선택한다.
예를 들어 앞에서 예를 들었던 정기예금투자와 주식투자에서 각각의 투자효용을 구해보자.
먼저 정기예금의 투자효용을 구해보면 다음과 같다.

주식의 투자효용을 크게 위험회피정도에 따라 위험회피형, 위험중립형, 위험선호형으로 나누어볼 때 다음과 같이 계산할 수 있다.
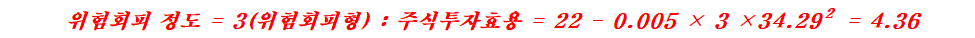

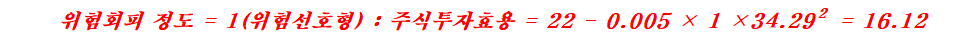
위험회피형 투자자는 비록 위험프리미엄이 12%일지라도 효용이 4.36으로서 정기예금 투자효용 10보다 작기 때문에 투자하는 것보다는 정기예금에 투자하려고 할 것이다. 위험선호형 투자자는 정기예금에 투자하는 것보다는 주식에 투자하는 것이 효용이 더 크므로 위험을 감수하고서라도 주식에 투자한다.
한편 같은 위험회정도라도 같은 효용을 제공하는 투자 포트폴리오가 존대하므로, 투자자는 비록 각 투자 포트폴리오가 서로 다른 기대이익과 위험을 갖더라도 선택에 대해 무차별할 것이다. 이와 같이 같은 효용의 포트폴리오를 연결한 곡선을 무차별곡선(indifference curve)이라한다.
아래의 표와 같이 위험회피정도를 4라고 할 때 각기 다른 기대이익과 위험수준에서 효용은 한결같이 2로서 같다.

개별자산 위험과 포트폴리오 위험
개별자산의 위험 크기는 반드시 포트폴리오 위험 크기와 같은 것은 아니다. 개별자산의 위험 크기는 일단 포트폴리오에 편입되면 전혀 다른 크기를 가진다. 예를 들어, 우산을 생산하는 회사와 선탠(suntan)로션을 생산하는 회사가 있다고 하자. 여름 한철 비가 오고 오지 않음에 따라 각 회사의 수익은 큰 영향을 받으며, 따라서 수익률 편차 또한 매우 클 것이다. 한 가지 분명한 것은 여름에 비가 많이 오면 우산회사는 이익은 많으나 선탠로션회사는 손해를 보는 등 두 회사의 성과가 서로 정반대로 움직인다는 점이다. 이와 같은 수익률 움직임은 두 회사가 정반대로 나타날 것이다.
만약 이 두 회사들을 모두 포함하는 포트폴리오를 구성한다면 비가 오든 오지 않든 일정한 이익을 확보할 수 있을 것이며, 포트폴리오의 위험은 거의 없다고 볼 수 있다. 이 포트폴리오의 수익률 움직임은 다음과 같이 평행선을 그릴 것이다.
이와 같이 개별자산으로서는 위험이 크지만 포트폴리오를 구성했을 때 개별자산의 위험은 별 문제가 되지 않는 경우가 많으므로, 어느 개별자산의 위험은 반드시 포트폴리오 입장에서 평가되어야 한다. 포트폴리오 위험을 관리하는 투자전략으로서 헷징(hedging)과 분산(diversification)이 있다. [헷징(hedging)]은 위에서 예를 든 우산회사와 선탠로션회사와 같이 어느 한 개별자산의 성과가 다른 개별자산에서 발생하는 위험을 제거해 주는 효과를 가진 포트폴리오이다. [분산(diversification)]은 "계란들을 한 바구니에 넣지 말라(Don't put one's eggs in a basket)"는 투자속담과 같이 투자대상을 어느 한 개별주식에 한정시키지 않고 여러 주식들에게 분산하여 투자함으로써 어느 한 개별주식에서 발생하는 위험을 희석시키는 것을 말한다.
'경영관리 > 투자이론' 카테고리의 다른 글
| 주식사는법)무위험자산과 위험감소에 대해 알아보자.(1) (18) | 2021.08.05 |
|---|---|
| 주식사는법)top-down 투자결정 (15) | 2021.08.04 |
| 주식사는법)증권투자의 위험에 대해 알아보자.(1) (4) | 2021.08.02 |
| 주식사는법) 증권시장지표에 대해 알아보자.(2) (13) | 2021.08.01 |
| 주식사는법) 증권시장지표에 대해 알아보자.(1) (2) | 2021.07.31 |





댓글 영역